How a 1:4 Guanella-Balun (Current-Balun) Operates – ByJerry Sodus, KM3K
1. The purpose of this article is to show how a 1:4 Guanella (current)-balun changes an impedance level by a multiplier of four; for example, 50-ohm coax to a 200-ohm antenna.
Although this is not a “how to make the balun” article, some design information is given for completeness.
2. Also, just to let you know…the Guanella (current)-balun can be turned around to go the other way; for example, a 50-ohm coax can be changed down to 12.5-ohm (say for a Yagi-antenna or a vertical-antenna). We’ll cover this later in paragraph #12.
3. BTW, Guanella came up with this idea in 1944.
In 1985, Roy W7EL gave Guanella’s idea the name “current-balun” because the balun’s output supplies equal current into/out of the output pins and that is a good thing.
4. It is important to put out of your mind any idea about flux-linkages and conventional-transformer action. Those concepts have nothing to do with this article.
5. The 1:4 Guanella (current)-balun is made from two 1:1 Guanella (current)-baluns.
Except for winding direction, they should be as identical in construction as possible to minimize any variation in signal delays; variations will increase signal loss at the higher frequencies.
6a. The 1:1 Guanella (current)-balun can be made up in several different ways:
A) coiling coax,
B) winding a transmission-line (coax or two-wire) on a toroid-core or rod; ferrite core/rod preferred,
C) threading coax thru ferrite-beads.
6b. Figure 1 has the usual schematic used for a 1:1 current-balun.
6c. To emphasize that the transmission-line mode is working here, lets use the schematic as in Figure 2.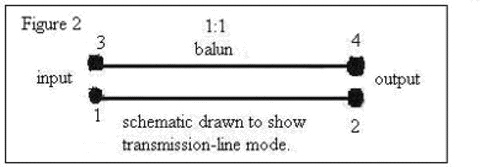
6d. Here is a key point.
We’ll assume that any signal loss thru the balun will be small enough that we can ignore it.
So, whatever voltage is at the input of the 1:1 balun is what we’ll see at its output.
In other words, we assume the signal’s voltage-level is not attenuated by the 1:1 balun.
In practice, we can approach this goal by using high-quality transmission-line and keeping its length short.
7. You connect up the baluns in this way as shown in Figure 3 below.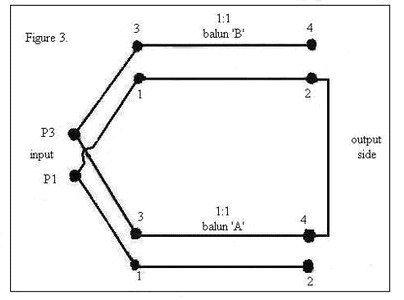
7a. The inputs are in parallel.
That means that any current going into terminal P3 splits in two, half goes up to terminal 3 and the other half will go down to the other terminal 3. At terminal P1, the currents coming out of each terminal 1 combine at P1 to flow back to where it started. Although P1 and P3 are where we will eventually the feed-line from the transmitter when we use the balun, for us right now, the feed-line is not connected.
7b. The outputs are in series.
Notice that if we were to connect an ohmmeter to P1 and P3 at this time, we’d read a short-circuit.
7c. Next connect a load ‘RL’, which we assume is a just a resistor for our purposes at this time. See Figure 4.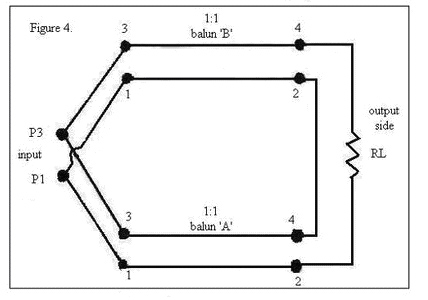
You may recall that a resonant-antenna is just a resistor, in other words, a pure resistance (no reactance). It’s interesting that, in Figure 4, the current going around the “inside-loop” never gets to the load RL. The “inside-loop” is from P3 going down to balun-A’s terminal 3, then to terminal 4, up to balun-B’s terminal 2, over to terminal 1 and then to terminal P1.
8. There is a term “input impedance” and we’ll use the symbol “Zin” for it.
In case “input impedance” is a new idea for some, here is a short explanation…
For us electronic folks, it is the value of impedance we’d measure at a test-frequency if we could connect up a special kind of alternating-current ohmmeter to terminals P1 and P3 in Figure 4. That value of Zin would replace the entire circuit to the right of P1 and P3.
For us right now, we are only concerned with the idea of “input impedance” and not with any actual value.
9. We’ll use the schematic in Figure 5 to find the power going into Zin.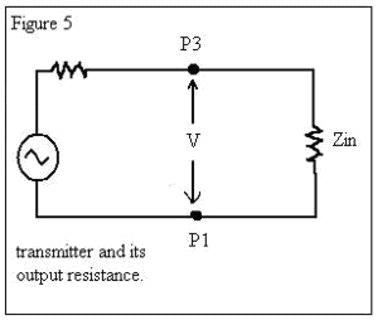
A key point here is to remember this is really the power going into the input of the 1:4 balun (at P1 & P3). In Figure 5, we are not concerned with the transmitter or its output-resistance. All we really care about is that there is Zin and a voltage across it; we’ll call that voltage “V”.
Recall that power going into a resistor is equal to ‘the voltage across the resistor’ times ‘the voltage across the resistor’ divided by ‘that resistance’.
So using our symbols, we can write the “power into the 1:4 balun” equals “V times V divided by Zin”.
10. Next we need the power going into the load RL. So, we need to know the voltage across RL. Here is how we’ll figure out what its value is.
10a. Recall that the voltage across P1 and P3 is V.
This is the same voltage across pins 1 and 3 at each of the 1:1 baluns.
10b. In step 6d, it is written that the same voltage V will be at each output of the 1:1 baluns.
10c. Step 7b has the outputs of the 1:1 baluns connected in series. So this means V plus V equals 2V is across the load RL. (If you have trouble understanding this, perhaps this may help. Just for now, pretend that each 1:1 balun output is a battery. So we have two batteries connected in series; just like in a flashlight and the light-bulb is the load. If each battery is 1.5 volts, we’d have 1.5 volts plus 1.5 volts equals 3 volts across the load.)
10d. The “power going into RL” is “2V times 2V divided by RL”.
11a. Now we are at the KEY section; the reason for this article. We are assuming there is no power lost in the baluns and that is a reasonable approximation throughout most of the 1:4 balun’s passband. We can write…”POWER INTO THE 1:4 BALUN” equals “POWER GOING INTO RL”. Paragraph 9 gives the “power into the 1:4 balun”.Paragraph 10d gives us the “power going into RL”, so we can write here… “V times V divided by Zin” equals “2V times 2V divided by RL”. Doing all the algebra, we come up with …..”RL equals 4 times Zin”. So we have proved we have a 1:4 impedance-ratio.
11b. An example ……….if Zin is 50-ohms, then RL is 200-ohms.
11c. Another example…..if Zin is 75-ohms, then RL is 300-ohms.
12 If we turn the 1:4 balun around to get a 4:1 balun, we can step-down in impedance.
For example, 50-ohms divided by 4 equals 12.5-ohms (maybe for a Yagi antenna); see Figure 6.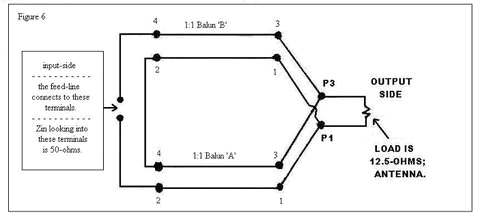
13. Comments about the transmission-line used in a 1:1 Guanella (current)-balun:
13a. The value of its characteristic-impedance Z0 (that is Z and a zero; pronounced Zee naught) is important.
13b. The 1:4 balun has a low impedance side and a high impedance side. Whatever the high impedance side is, divided that value by two and that is the characteristic impedance to use in the 1:1 Guanella (current)-balun.
13c. Here are examples of some values for 1:4 Guanella-baluns…
for 50-ohm to 200-ohm, Z0 is 100-ohm.
for 75-ohm to 300-ohm, Z0 is 150-ohm.
for 50-ohm to 12.5-ohm, Z0 is 25-ohm.
13d. You can make your own transmission-line (two-wire or coax); see Sevick’s “Transmission-Line-Transformers”.
13e. The more you deviate from the design Z0, the more power you lose at higher frequencies.
14a. The 1:4 concept can be extended to other ratios like 1:9 and 1:16 and 1:25.
14b. But more 1:1 baluns are needed; the 1:9 uses three; the 1:16 uses four, etc.
14c. The Z0 formula changes also; for 1:9, divide the high impedance by three; divide by four for the 1:16.
15. For completeness sake….it is possible to make a 1:4 Guanella-balun on just one core (in other words, two 1:1 baluns on one core paying proper attention to all pertinent details); however, that design approach should not be used if the load is grounded (virtually or actually) at its center point.
I hope this article is of some benefit in explaining how the 1:4 Guanella (current)-balun “does its thing”.
73 Jerry Sodus, KM3K
South-Mountain-Radio-Amateurs Club